第五节  隐函数的求导公式

一 原理、公式和方法

隐函数存在定理1  设函数在点的某一邻域内具有连续的偏导数，且，而方程在点的某一邻域内恒能唯一确定一个单值连续且具有连续导数的函数，它满足条件，并有

．

隐函数存在定理2  设函数在点的某一邻域内具有连续的偏导数，且，则方程在点的某一邻域内恒能唯一确定一个单值连续且具有连续偏导数的函数，它满足条件，并有

．

隐函数存在定理3  设、在点的某一邻域内具有对各个变量的连续偏导数，又，且偏导数所组成的函数行列式(或称雅可比(Jacobi)式)：

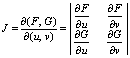
在点不等于零，则方程组在点的某一邻域内恒能唯一确定一组单值连续且具有连续偏导数的函数，它们满足条件，并有

， ，      

，．

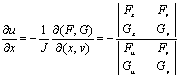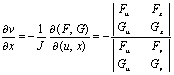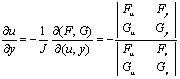二 重点、难点分析

隐函数的求导方法是本章的重点内容，计算隐函数的二阶导数（偏导数）是本章的难点内容。

利用隐函数存在定理2计算由方程确定的隐函数的偏导数时，需特别注意：

1）求偏导数时，在函数中，将看作常量，对求导数。计算和时，应注意同样的问题。

2）计算二阶偏导数时，对一阶偏导数关于自变量求偏导数，其中的是的二元函数。

隐函数存在定理2、3可以推广到更多个方程和变量的情形。

三 典型例题分析

例1  设，求．

解  设，则．应用隐函数存在定理2，得

．

再对求偏导数，得

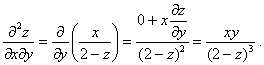
例2 设，求和．

解  此题可直接利用隐函数存在定理3中的公式，但也可依照推导该公式的方法来求解．下面我们用后一种方法来做．

将所给方程的两边对偏导数并移项，得

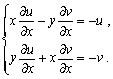
在的条件下，

，    ．

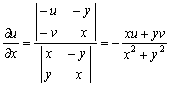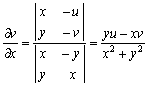将所给方程的两边对偏导数，用同样方法在的条件下可得

，．