要判断一个集合A是否为可数集，大致有如下方法：

方法一.  按照可数集的定义， 若A为有限集，则A一定是可数集，否则若A可与自然数集之间存在一个1-1映射，则A为可数集。

方法二.  若A中所有元素可某种规律排列出来，则A是可数集。

方法三.  若A是两个不相交的可数集的并集，则A是可数集。

方法四.  若A是某个已知是可数集的集合的子集，则A是可数集。

方法五.  若A是可数无穷多个可数集合的并集，则A是可数集合。

方法六.  若A是两个可数无穷集合的笛卡儿乘积，则A是可数集合。

例1.2.5  证明全体整数做成的集合是可数集。

证法一：建立自然数集到整数集的映射σ如下：
          

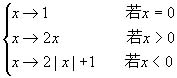
显然，σ是自然数集到整数集的1-1映射。因此，整数集是可数集。

证法二：因整数集可排成如下次序：

{0，1，-1，2，-2，3，-3，……}，

所以，整数集是可数集。

证法三：因自然数集{1，2，3，……}是可数集，所以将该集合中每个元素加负号得到的集合{-1，-2，-3，……}亦是可数集，{0}是有限集，当然可数，因此，这三个互不相交的可数集合的并集，即整数集，仍是可数集。

证法四：若已知有理数集合是可数集，则由于整数集是有理数集合的子集，因此，整数集是可数集。

由此例和方法五还知，Z×Z也是可数集。